Diffraction and optical resolution

Diffraction is the process by which light interference is most commonly observed. The effect was first described in 1665 by Francesco Maria Grimaldi, who also coined the term from the Latin diffringere, ‘to break into pieces.Later that century, Robert Hooke and Isaac Newton also described phenomena now known to be diffraction in Newton’s rings while James Gregory recorded his observations of diffraction patterns from bird feathers.

The first physical optics model of diffraction that relied on the Huygens–Fresnel principle was developed in 1803 by Thomas Young in his interference experiments with the interference patterns of two closely spaced slits. Young showed that his results could only be explained if the two slits acted as two unique sources of waves rather than corpuscles. In 1815 and 1818, Augustin-Jean Fresnel firmly established the mathematics of how wave interference can account for diffraction.

diffraction-1

Diffraction on two slits separated by distance d. The bright fringes occur along lines where black lines intersect with black lines and white lines intersect with white lines. These fringes are separated by angle θ and are numbered as order n .

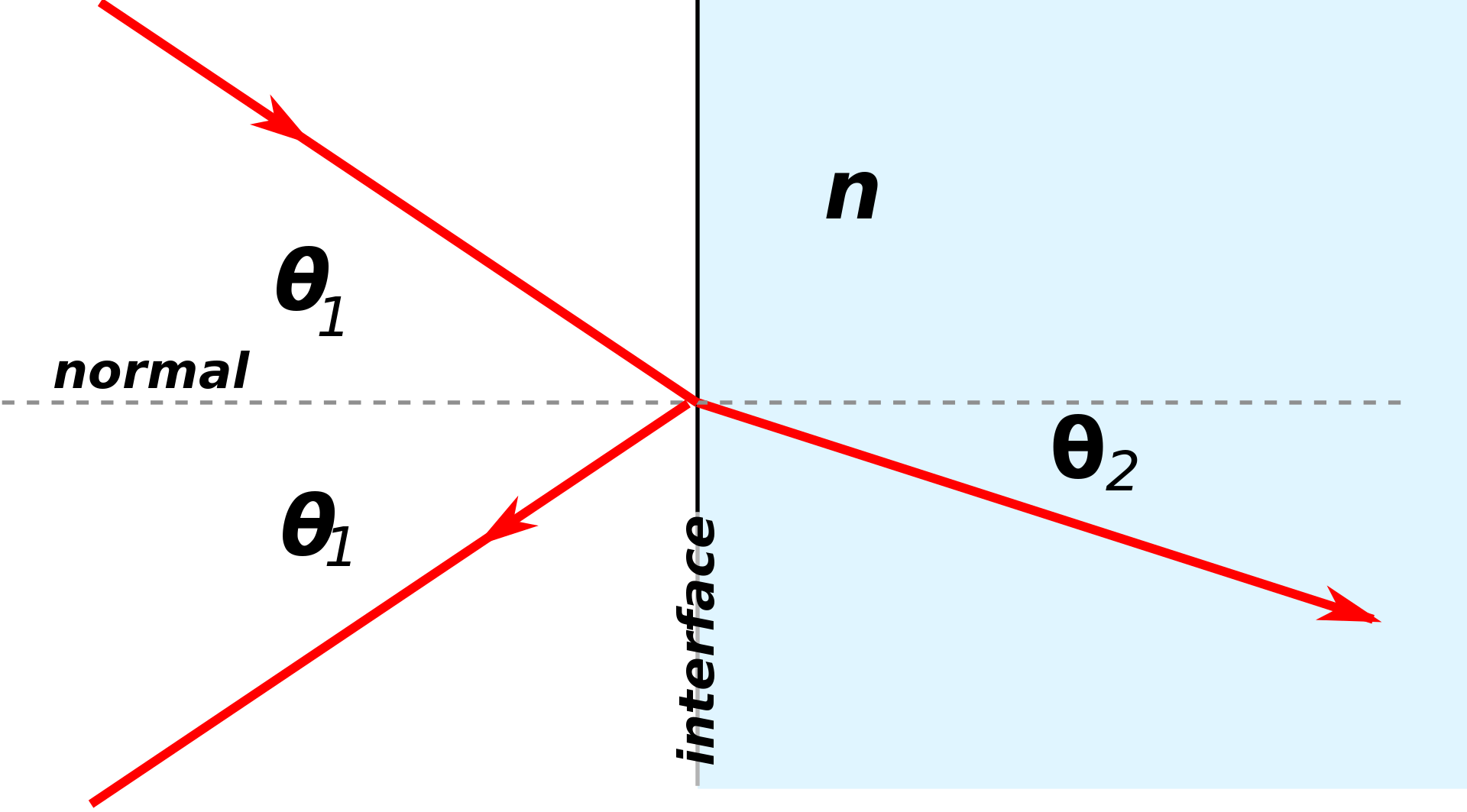
The simplest physical models of diffraction use equations that describe the angular separation of light and dark fringes due to light of a particular wavelength (λ). In general, the equation takes the form

where  d  is the separation between two wavefront sources (in the case of Young’s experiments, it was two slits),θ is the angular separation between the central fringe and the  m  th order fringe, where the central maximum is m=0

This equation is modified slightly to take into account a variety of situations such as diffraction through a single gap, diffraction through multiple slits, or diffraction through a diffraction grating that contains a large number of slits at equal spacing.More complicated models of diffraction require working with the mathematics of Fresnel or Fraunhofer diffraction.

X-ray diffraction makes use of the fact that atoms in a crystal have regular spacing at distances that are on the order of one angstrom. To see diffraction patterns, x-rays with similar wavelengths to that spacing are passed through the crystal. Since crystals are three-dimensional objects rather than two-dimensional gratings, the associated diffraction pattern varies in two directions according to Bragg reflection, with the associated bright spots occurring in unique patterns and d  being twice the spacing between atoms.

Diffraction effects limit the ability of an optical detector to optically resolve separate light sources. In general, light that is passing through an aperture will experience diffraction and the best images that can be created (as described in diffraction-limited optics) appear as a central spot with surrounding bright rings, separated by dark nulls; this pattern is known as an Airy pattern, and the central bright lobe as an Airy disk. The size of such a disk is given by

where θ is the angular resolution, λ is the wavelength of the light, and D is the diameter of the lens aperture. If the angular separation of the two points is significantly less than the Airy disk angular radius, then the two points cannot be resolved in the image, but if their angular separation is much greater than this, distinct images of the two points are formed and they can therefore be resolved. Rayleigh defined the somewhat arbitrary “Rayleigh criterion” that two points whose angular separation is equal to the Airy disk radius (measured to first null, that is, to the first place where no light is seen) can be considered to be resolved. It can be seen that the greater the diameter of the lens or its aperture, the finer the resolution.Interferometry, with its ability to mimic extremely large baseline apertures, allows for the greatest angular resolution possible.

For astronomical imaging, the atmosphere prevents optimal resolution from being achieved in the visible spectrum due to the atmospheric scattering and dispersion which cause stars to twinkle. Astronomers refer to this effect as the quality of astronomical seeing. Techniques known as adaptive optics have been used to eliminate the atmospheric disruption of images and achieve results that approach the diffraction limit.

/0 Comments/by

Superposition and interference

In the absence of nonlinear effects, the superposition principle can be used to predict the shape of interacting waveforms through the simple addition of the disturbances. This interaction of waves to produce a resulting pattern is generally termed “interference” and can result in a variety of outcomes. If two waves of the same wavelength and frequency are in phase, both the wave crests and wave troughs align. This results in constructive interference and an increase in the amplitude of the wave, which for light is associated with a brightening of the waveform in that location. Alternatively, if the two waves of the same wavelength and frequency are out of phase, then the wave crests will align with wave troughs and vice versa. This results in destructive interference and a decrease in the amplitude of the wave, which for light is associated with a dimming of the waveform at that location. See below for an illustration of this effect.

Superposition and interference

                                               Two waves in phase                                                                                                       Two waves 180° out of phase

Since the Huygens–Fresnel principle states that every point of a wavefront is associated with the production of a new disturbance, it is possible for a wavefront to interfere with itself constructively or destructively at different locations producing bright and dark fringes in regular and predictable patterns.Interferometry is the science of measuring these patterns, usually as a means of making precise determinations of distances or angular resolutions. The Michelson interferometer was a famous instrument which used interference effects to accurately measure the speed of light.

The appearance of thin films and coatings is directly affected by interference effects. Antireflective coatings use destructive interference to reduce the reflectivity of the surfaces they coat, and can be used to minimise glare and unwanted reflections. The simplest case is a single layer with a thickness of one-fourth the wavelength of incident light. The reflected wave from the top of the film and the reflected wave from the film/material interface are then exactly 180° out of phase, causing destructive interference. The waves are only exactly out of phase for one wavelength, which would typically be chosen to be near the centre of the visible spectrum, around 550 nm. More complex designs using multiple layers can achieve low reflectivity over a broad band, or extremely low reflectivity at a single wavelength.

Constructive interference in thin films can create a strong reflection of light in a range of wavelengths, which can be narrow or broad depending on the design of the coating. These films are used to make dielectric mirrors, interference filters, heat reflectors, and filters for colour separation in colour television cameras. This interference effect is also what causes the colourful rainbow patterns seen in oil slicks.

/0 Comments/by

Physical optics

In physical optics, light is considered to propagate as a wave. This model predicts phenomena such as interference and diffraction, which are not explained by geometric optics. The speed of light waves in air is approximately 3.0×108 m/s (exactly 299,792,458 m/s in vacuum). The wavelength of visible light waves varies between 400 and 700 nm, but the term “light” is also often applied to infrared (0.7–300 μm) and ultraviolet radiation (10–400 nm).

The wave model can be used to make predictions about how an optical system will behave without requiring an explanation of what is “waving” in what medium. Until the middle of the 19th century, most physicists believed in an “ethereal” medium in which the light disturbance propagated.The existence of electromagnetic waves was predicted in 1865 by Maxwell’s equations. These waves propagate at the speed of light and have varying electric and magnetic fields which are orthogonal to one another, and also to the direction of propagation of the waves.Light waves are now generally treated as electromagnetic waves except when quantum mechanical effects have to be considered.

Modelling and design of optical systems using physical optics

Many simplified approximations are available for analysing and designing optical systems. Most of these use a single scalar quantity to represent the electric field of the light wave, rather than using a vector model with orthogonal electric and magnetic vectors. The Huygens–Fresnel equation is one such model. This was derived empirically by Fresnel in 1815, based on Huygens’ hypothesis that each point on a wavefront generates a secondary spherical wavefront, which Fresnel combined with the principle of superposition of waves. The Kirchhoff diffraction equation, which is derived using Maxwell’s equations, puts the Huygens-Fresnel equation on a firmer physical foundation. Examples of the application of Huygens–Fresnel principle can be found in the articles on diffraction and Fraunhofer diffraction.

More rigorous models, involving the modelling of both electric and magnetic fields of the light wave, are required when dealing with materials whose electric and magnetic properties affect the interaction of light with the material. For instance, the behaviour of a light wave interacting with a metal surface is quite different from what happens when it interacts with a dielectric material. A vector model must also be used to model polarised light.

Numerical modeling techniques such as the finite element method, the boundary element method and the transmission-line matrix method can be used to model the propagation of light in systems which cannot be solved analytically. Such models are computationally demanding and are normally only used to solve small-scale problems that require accuracy beyond that which can be achieved with analytical solutions.

All of the results from geometrical optics can be recovered using the techniques of Fourier optics which apply many of the same mathematical and analytical techniques used in acoustic engineering and signal processing.

Gaussian beam propagation is a simple paraxial physical optics model for the propagation of coherent radiation such as laser beams. This technique partially accounts for diffraction, allowing accurate calculations of the rate at which a laser beam expands with distance, and the minimum size to which the beam can be focused. Gaussian beam propagation thus bridges the gap between geometric and physical optics.

/0 Comments/by

Refractions

Refraction occurs when light travels through an area of space that has a changing index of refraction; this principle allows for lenses and the focusing of light. The simplest case of refraction occurs when there is an interface between a uniform medium with index of refraction n1 and another medium with index of refraction n2. In such situations, Snell’s Law describes the resulting deflection of the light ray:

 

where θ1 and θ2 are the angles between the normal (to the interface) and the incident and refracted waves, respectively.

The index of refraction of a medium is related to the speed, v, of light in that medium by

,

where c is the speed of light in vacuum.

Snell’s Law can be used to predict the deflection of light rays as they pass through linear media as long as the indexes of refraction and the geometry of the media are known. For example, the propagation of light through a prism results in the light ray being deflected depending on the shape and orientation of the prism. In most materials, the index of refraction varies with the frequency of the light. Taking this into account, Snell’s Law can be used to predict how a prism will disperse light into a spectrum. The discovery of this phenomenon when passing light through a prism is famously attributed to Isaac Newton.

Some media have an index of refraction which varies gradually with position and, therefore, light rays in the medium are curved. This effect is responsible for mirages seen on hot days: a change in index of refraction air with height causes light rays to bend, creating the appearance of specular reflections in the distance (as if on the surface of a pool of water). Optical materials with varying indexes of refraction are called gradient-index (GRIN) materials. Such materials are used to make gradient-index optics.

For light rays travelling from a material with a high index of refraction to a material with a low index of refraction, Snell’s law predicts that there is no θ2 when θ1 is large. In this case, no transmission occurs; all the light is reflected. This phenomenon is called total internal reflection and allows for fibre optics technology. As light travels down an optical fibre, it undergoes total internal reflection allowing for essentially no light to be lost over the length of the cable.

/0 Comments/by

Reflections

Reflections can be divided into two types: specular reflection and diffuse reflection. Specular reflection describes the gloss of surfaces such as mirrors, which reflect light in a simple, predictable way. This allows for the production of reflected images that can be associated with an actual (real) or extrapolated (virtual) location in space. Diffuse reflection describes non-glossy materials, such as paper or rock. The reflections from these surfaces can only be described statistically, with the exact distribution of the reflected light depending on the microscopic structure of the material. Many diffuse reflectors are described or can be approximated by Lambert’s cosine law, which describes surfaces that have equal luminance when viewed from any angle. Glossy surfaces can give both specular and diffuse reflection.

Reflection-1

In specular reflection, the direction of the reflected ray is determined by the angle the incident ray makes with the surface normal, a line perpendicular to the surface at the point where the ray hits. The incident and reflected rays and the normal lie in a single plane, and the angle between the reflected ray and the surface normal is the same as that between the incident ray and the normal. This is known as the Law of Reflection.

For flat mirrors, the law of reflection implies that images of objects are upright and the same distance behind the mirror as the objects are in front of the mirror. The image size is the same as the object size. The law also implies that mirror images are parity inverted, which we perceive as a left-right inversion. Images formed from reflection in two (or any even number of) mirrors are not parity inverted. Corner reflectors produce reflected rays that travel back in the direction from which the incident rays came.This is called retroreflection.

Mirrors with curved surfaces can be modelled by ray tracing and using the law of reflection at each point on the surface. For mirrors with parabolic surfaces, parallel rays incident on the mirror produce reflected rays that converge at a common focus. Other curved surfaces may also focus light, but with aberrations due to the diverging shape causing the focus to be smeared out in space. In particular, spherical mirrors exhibit spherical aberration. Curved mirrors can form images with a magnification greater than or less than one, and the magnification can be negative, indicating that the image is inverted. An upright image formed by reflection in a mirror is always virtual, while an inverted image is real and can be projected onto a screen.

/0 Comments/by

History

Optics began with the development of lenses by the ancient Egyptians and Mesopotamians. The earliest known lenses, made from polished crystal, often quartz, date from as early as 2000 BC from Crete (Archaeological Museum of Heraclion, Greece). Lenses from Rhodes date around 700 BC, as do Assyrian lenses such as the Nimrud lens.The ancient Romans and Greeks filled glass spheres with water to make lenses. These practical developments were followed by the development of theories of light and vision by ancient Greek and Indian philosophers, and the development of geometrical optics in the Greco-Roman world. The word optics comes from the ancient Greek word ὀπτική (optikē), meaning “appearance, look”.

Greek philosophy on optics broke down into two opposing theories on how vision worked, the intromission theory and the emission theory.The intromission approach saw vision as coming from objects casting off copies of themselves (called eidola) that were captured by the eye. With many propagators including Democritus, Epicurus, Aristotle and their followers, this theory seems to have some contact with modern theories of what vision really is, but it remained only speculation lacking any experimental foundation.

Plato first articulated the emission theory, the idea that visual perception is accomplished by rays emitted by the eyes. He also commented on the parity reversal of mirrors in Timaeus.Some hundred years later, Euclid (4th–3rd century BC) wrote a treatise entitled Optics where he linked vision to geometry, creating geometrical optics.He based his work on Plato’s emission theory wherein he described the mathematical rules of perspective and described the effects of refraction qualitatively, although he questioned that a beam of light from the eye could instantaneously light up the stars every time someone blinked.Euclid stated the principle of shortest trajectory of light, and considered multiple reflections on flat and spherical mirrors. Ptolemy, in his treatise Optics, held an extramission-intromission theory of vision: the rays (or flux) from the eye formed a cone, the vertex being within the eye, and the base defining the visual field. The rays were sensitive, and conveyed information back to the observer’s intellect about the distance and orientation of surfaces. He summarized much of Euclid and went on to describe a way to measure the angle of refraction, though he failed to notice the empirical relationship between it and the angle of incidence. Plutarch (1st–2nd century AD) described multiple reflections on spherical mirrors and discussed the creation of magnified and reduced images, both real and imaginary, including the case of chirality of the images

In the 13th century in medieval Europe, English bishop Robert Grosseteste wrote on a wide range of scientific topics, and discussed light from four different perspectives: an epistemology of light, a metaphysics or cosmogony of light, an etiology or physics of light, and a theology of light, basing it on the works of Aristotle and Platonism. Grosseteste’s most famous disciple, Roger Bacon, wrote works citing a wide range of recently translated optical and philosophical works, including those of Alhazen, Aristotle, Avicenna, Averroes, Euclid, al-Kindi, Ptolemy, Tideus, and Constantine the African. Bacon was able to use parts of glass spheres as magnifying glasses to demonstrate that light reflects from objects rather than being released from them.

The first wearable eyeglasses were invented in Italy around 1286. This was the start of the optical industry of grinding and polishing lenses for these “spectacles”, first in Venice and Florence in the thirteenth century,and later in the spectacle making centres in both the Netherlands and Germany.Spectacle makers created improved types of lenses for the correction of vision based more on empirical knowledge gained from observing the effects of the lenses rather than using the rudimentary optical theory of the day (theory which for the most part could not even adequately explain how spectacles worked).This practical development, mastery, and experimentation with lenses led directly to the invention of the compound optical microscope around 1595, and the refracting telescope in 1608, both of which appeared in the spectacle making centres in the Netherland

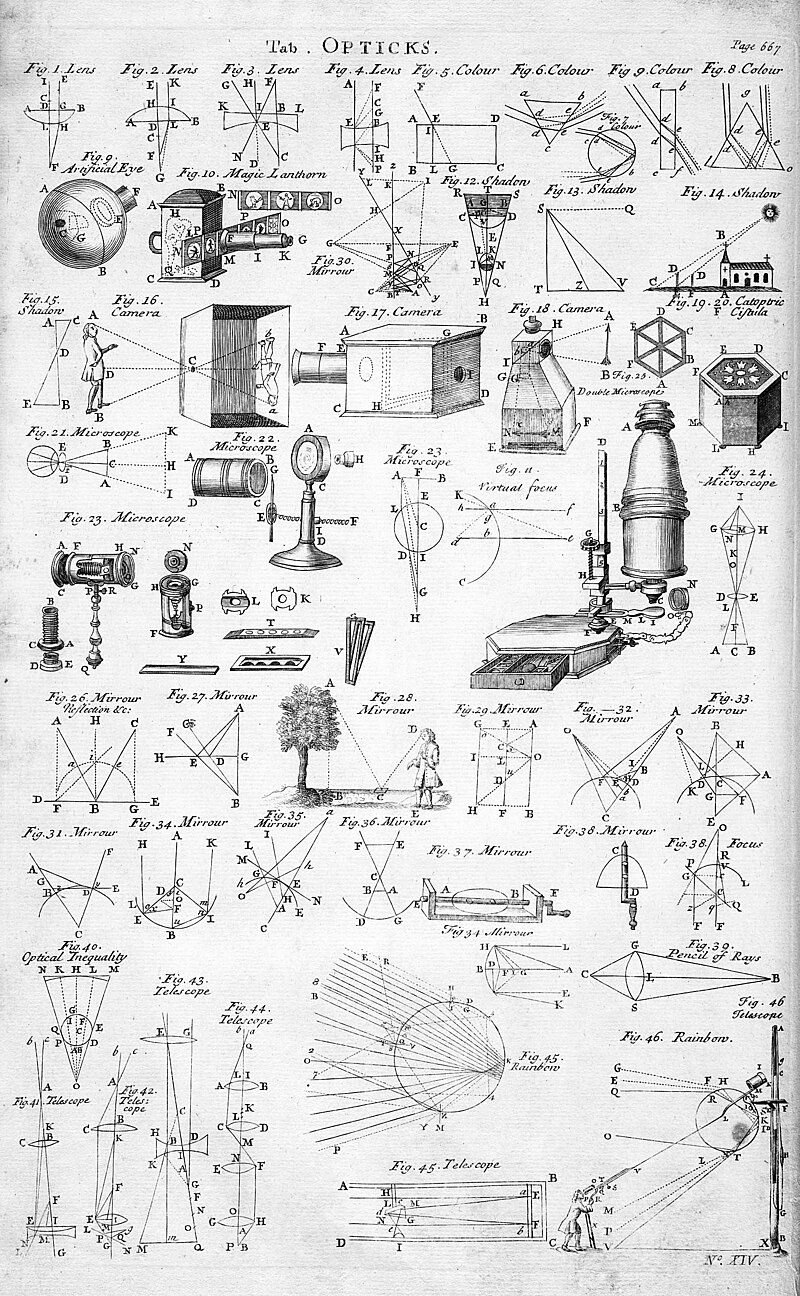
optics-1In the early 17th century, Johannes Kepler expanded on geometric optics in his writings, covering lenses, reflection by flat and curved mirrors, the principles of pinhole cameras, inverse-square law governing the intensity of light, and the optical explanations of astronomical phenomena such as lunar and solar eclipses and astronomical parallax. He was also able to correctly deduce the role of the retina as the actual organ that recorded images, finally being able to scientifically quantify the effects of different types of lenses that spectacle makers had been observing over the previous 300 years.After the invention of the telescope, Kepler set out the theoretical basis on how they worked and described an improved version, known as the Keplerian telescope, using two convex lenses to produce higher magnification.Optics-2

Optical theory progressed in the mid-17th century with treatises written by philosopher René Descartes, which explained a variety of optical phenomena including reflection and refraction by assuming that light was emitted by objects which produced it.This differed substantively from the ancient Greek emission theory. In the late 1660s and early 1670s, Isaac Newton expanded Descartes’s ideas into a corpuscle theory of light, famously determining that white light was a mix of colours that can be separated into its component parts with a prism. In 1690, Christiaan Huygens proposed a wave theory for light based on suggestions that had been made by Robert Hooke in 1664. Hooke himself publicly criticised Newton’s theories of light and the feud between the two lasted until Hooke’s death. In 1704, Newton published Opticks and, at the time, partly because of his success in other areas of physics, he was generally considered to be the victor in the debate over the nature of light.

optics-3

Newtonian optics was generally accepted until the early 19th century when Thomas Young and Augustin-Jean Fresnel conducted experiments on the interference of light that firmly established light’s wave nature. Young’s famous double slit experiment showed that light followed the superposition principle, which is a wave-like property not predicted by Newton’s corpuscle theory. This work led to a theory of diffraction for light and opened an entire area of study in physical optics.Wave optics was successfully unified with electromagnetic theory by James Clerk Maxwell in the 1860s.

The next development in optical theory came in 1899 when Max Planck correctly modelled blackbody radiation by assuming that the exchange of energy between light and matter only occurred in discrete amounts he called quanta.In 1905, Albert Einstein published the theory of the photoelectric effect that firmly established the quantization of light itself.In 1913, Niels Bohr showed that atoms could only emit discrete amounts of energy, thus explaining the discrete lines seen in emission and absorption spectra.The understanding of the interaction between light and matter that followed from these developments not only formed the basis of quantum optics but also was crucial for the development of quantum mechanics as a whole. The ultimate culmination, the theory of quantum electrodynamics, explains all optics and electromagnetic processes in general as the result of the exchange of real and virtual photons.Quantum optics gained practical importance with the inventions of the maser in 1953 and of the laser in 1960.

Following the work of Pctromagnetic field in the 1950s and 1960s to gain a more detailed understanding of photodetection and the statistics of light.aul Dirac in quantum field theory, George Sudarshan, Roy J. Glauber, and Leonard Mandel applied quantum theory to the electrodynamics, explains all optics and electromagnetic processes in general as the result of the exchange of real and virtual photons.Quantum optics gained practical importance with the inventions of the maser in 1953 and of the laser in 1960.

Following the work of Paul Dirac in quantum field theory, George Sudarshan, Roy J. Glauber, and Leonard Mandel applied quantum theory to the electromagnetic field in the 1950s and 1960s to gain a more detailed understanding of photodetection and the statistics of light.

/0 Comments/by

A device that produces converging or diverging light rays due to refraction is known as a lens. Lenses are characterized by their focal length: a converging lens has positive focal length, while a diverging lens has negative focal length. Smaller focal length indicates that the lens has a stronger converging or diverging effect. The focal length of a simple lens in air is given by the lensmaker’s equation.

Ray tracing can be used to show how images are formed by a lens. For a thin lens in air, the location of the image is given by the simple equation

,

where S1 is the distance from the object to the lens, S2 is the distance from the lens to the image, and  f  is the focal length of the lens. In the sign convention used here, the object and image distances are positive if the object and image are on opposite sides of the lens.

Incoming parallel rays are focused by a converging lens onto a spot one focal length from the lens, on the far side of the lens. This is called the rear focal point of the lens. Rays from an object at a finite distance are focused further from the lens than the focal distance; the closer the object is to the lens, the further the image is from the lens.

With diverging lenses, incoming parallel rays diverge after going through the lens, in such a way that they seem to have originated at a spot one focal length in front of the lens. This is the lens’s front focal point. Rays from an object at a finite distance are associated with a virtual image that is closer to the lens than the focal point, and on the same side of the lens as the object. The closer the object is to the lens, the closer the virtual image is to the lens. As with mirrors, upright images produced by a single lens are virtual, while inverted images are real.

Lenses suffer from aberrations that distort images. Monochromatic aberrations occur because the geometry of the lens does not perfectly direct rays from each object point to a single point on the image, while chromatic aberration occurs because the index of refraction of the lens varies with the wavelength of the light.

/0 Comments/by

Geometrical optics

Geometry of reflection and refraction of light rays

Geometrical optics, or ray optics, describes the propagation of light in terms of “rays” which travel in straight lines, and whose paths are governed by the laws of reflection and refraction at interfaces between different media. These laws were discovered empirically as far back as 984 AD and have been used in the design of optical components and instruments from then until the present day. They can be summarised as follows:

When a ray of light hits the boundary between two transparent materials, it is divided into a reflected and a refracted ray.

The law of reflection says that the reflected ray lies in the plane of incidence, and the angle of reflection equals the angle of incidence.
The law of refraction says that the refracted ray lies in the plane of incidence, and the sine of the angle of incidence divided by the sine of the angle of refraction is a constant:
,

where n is a constant for any two materials and a given colour of light. If the first material is air or vacuum, n is the refractive index of the second material.

The laws of reflection and refraction can be derived from Fermat’s principle which states that the path taken between two points by a ray of light is the path that can be traversed in the least time.

Geometric optics is often simplified by making the paraxial approximation, or “small angle approximation”. The mathematical behaviour then becomes linear, allowing optical components and systems to be described by simple matrices. This leads to the techniques of Gaussian optics and paraxialray tracing, which are used to find basic properties of optical systems, such as approximate image and object positions and magnifications.

/0 Comments/by

Optics

Classical optics is divided into two main branches: geometrical (or ray) optics and physical (or wave) optics. In geometrical optics, light is considered to travel in straight lines, while in physical optics, light is considered as an electromagnetic wave.

Geometrical optics can be viewed as an approximation of physical optics that applies when the wavelength of the light used is much smaller than the size of the optical elements in the system being modelled.

Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviolet, and infrared light. Because light is an electromagnetic wave, other forms of electromagnetic radiation such as X-rays, microwaves, and radio waves exhibit similar properties.

optics-4

Most optical phenomena can be accounted for by using the classical electromagnetic description of light, however complete electromagnetic descriptions of light are often difficult to apply in practice. Practical optics is usually done using simplified models. The most common of these, geometric optics, treats light as a collection of rays that travel in straight lines and bend when they pass through or reflect from surfaces. Physical optics is a more comprehensive model of light, which includes wave effects such as diffraction and interference that cannot be accounted for in geometric optics. Historically, the ray-based model of light was developed first, followed by the wave model of light. Progress in electromagnetic theory in the 19th century led to the discovery that light waves were in fact electromagnetic radiation.

Stylised_atom_with_three_Bohr_model_orbits_and_stylised_nucleus.svg

Some phenomena depend on light having both wave-like and particle-like properties. Explanation of these effects requires quantum mechanics. When considering light’s particle-like properties, the light is modelled as a collection of particles called “photons”. Quantum optics deals with the application of quantum mechanics to optical systems.

Optical science is relevant to and studied in many related disciplines including astronomy, various engineering fields, photography, and medicine (particularly ophthalmology and optometry, in which it is called physiological optics). Practical applications of optics are found in a variety of technologies and everyday objects, including mirrors, lenses, telescopes, microscopes, lasers, and fibre optics.

 

/0 Comments/by